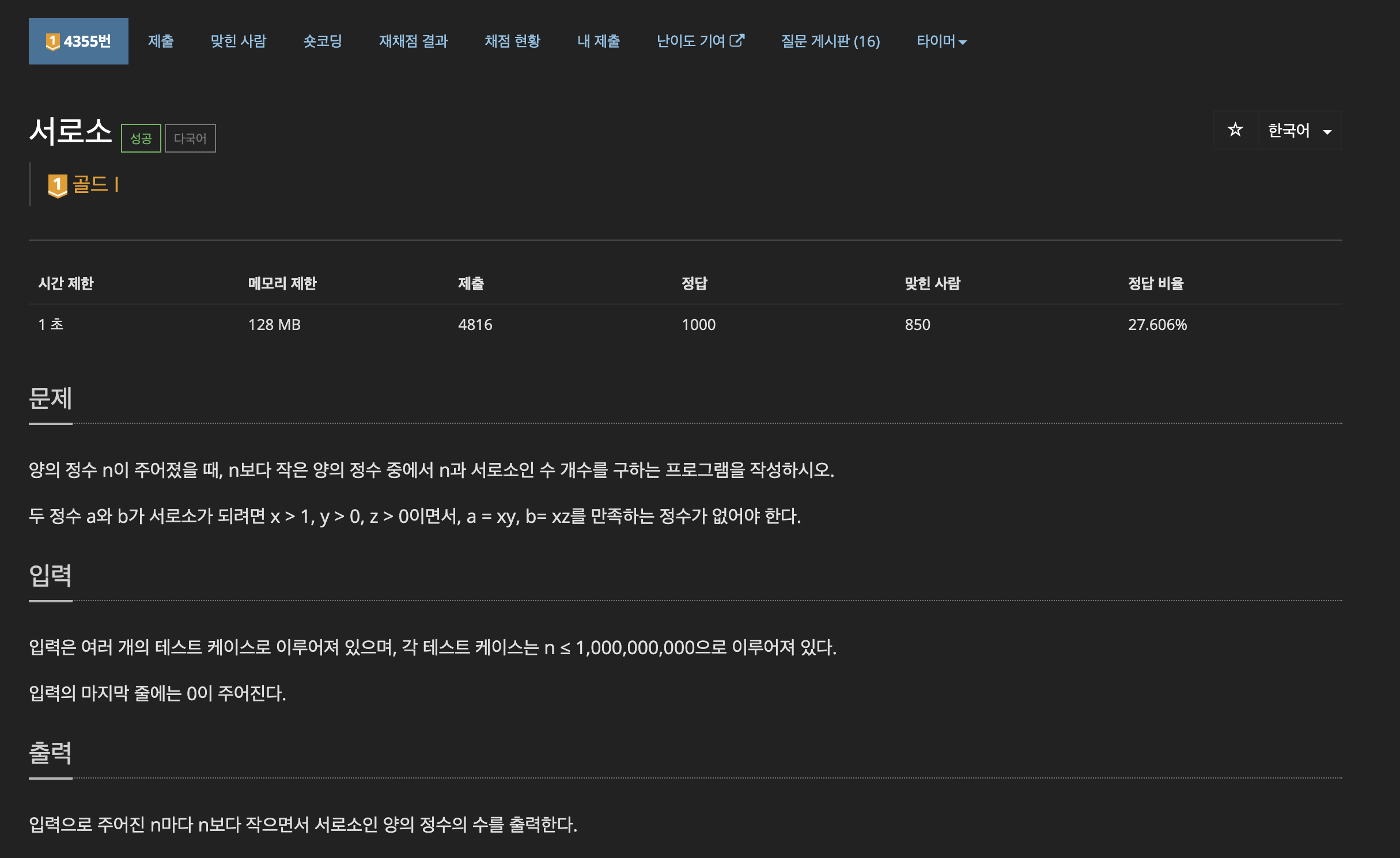
문제
https://www.acmicpc.net/problem/4355
| 시간 제한 | 메모리 제한 | solved.ac 티어 |
| 1초 | 128MB | 골드 1 |
풀이
오랜만에 밀린 문제 정리하기이다. 아마 내가 지금 당장 정리하고 싶다는 욕망이 드는 문제가 아니고선, 풀었던 문제를 알고리즘별로 묶어서 한번에 처리하지 않을까 싶다. 지금까지도 풀었던 최단경로 문제부터 정리했었다. 이번 문제가 알고리즘별로 묶어서 정리하는 그 시초가 될 것 같다. 이번 알고리즘은 오일러 피함수, 오일러 토션트함수이다. 사실 정수론, 해석학, 대수학등, 수학 과학을 꽤 좋아하는 입장에서, 수학적인 알고리즘도 굉장히 좋아한다. 뭐... 그걸 딥하게 파고들어서 이해하는건 별개의 몫이지만 말이다.
오일러 피함수는 자연수 n에 대해 자연수 n과 서로소인 n이하의 자연수의 개수를 구하는 정수론의 특수함수이다. 뭐... 증명은 차치하고 오일러 토션트 함수값을 구하는 건 굉장히 쉽다. n의 소인수 p1, p2...pk가 있으면 n의 오일러 피함수 값은 다음과 같이 구한다.
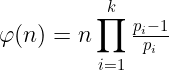
오일러 피함수의 간단한 특징을 살펴보고자 한다. 우선 소수에 관한 이야기이다. 소수 p에 대해 다음 두 식이 성립한다.
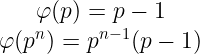
그리고 서로소인 두 정수 a, b는 다음 곱셈적 성질을 만족한다.
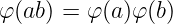
증명은 굳이 내가 할필요보다는 깔끔하게 잘 해두신분의 글을 참조하는게 좋을 것 같다. 언젠가엔 정수론을 좀 더 공부한 후, 나도 제대로 정리해두고자 한다. 일단 지금은 보류 ㅎㅎ..
https://blog.naver.com/yyhjin12/222864062441
오일러 피 함수(Euler's phi function)
오일러 피 함수에 대한 내용을 다룹니다. 오일러 피 함수는 기호로 아래와 같이 씁니다. phi라고 읽습니다....
blog.naver.com
오일러 피함수를 함수로 간단하게 구현하면 다음과 같을 것이다.
uint64_t sol(int n) {
uint64_t res = n;
for (int i = 2; i * i <= n; i++) {
// 소인수 발견
if (n % i == 0) {
res /= i;
res *= (i - 1);
}
// 소인수의 배수는 제거해야한다.
while (n % i == 0) n /= i;
}
// 처리되지 않은 낭믄 수는 소수이다.
if (n != 1) {
res /= n;
res *= (n - 1);
}
return res;
}
에라토스테네스의 체와 비슷한 과정을 적용시킨 코드이다. 우리가 알고자하는건 소인수이지 그냥 인수가 아니기 때문이다. 따라서 필요한 경우, 에라토스테네스의 체를 따로 작성하여 오일러 피함수에 적용할 수 있다. 이 경우에 좋은 점은, 오일러 피함수의 성질을 사용할 수 있다는 것이다. 만약에 우리가 알고자하는 n이 소수라면 바로 n-1을 return하면 되고, 그게 아니더라도, 소수중에서만 탐색하여 나누어 떨어지는 소인수를 찾을 수 있기 때문이다. 수가 매우 커지게 되면 이 방법도 불가능해지는데, 이때는 폴라드-로 알고리즘을 통해 더 빠르게 소인수를 찾은 후, 오일러 피함수를 적용시켜야 한다. 이러한 문제도 추후 풀이할 것이다.
일반적인 오일러 피함수의 경우 1의 오일러 피함수 값은 1이다. 1이하의 1과 서로소인 자연수는 1이 있기 때문이다. 하지만 이번 문제에서는 주어진 정수보다 작은 서로소의 개수를 구하라고 한다. 2 이상의 자연수들은 자기자신과는 서로소가 아니지만, 1의 경우는 자기 자신과 서로소이기 때문에, 이 부분을 추가해주어야 한다.
코드
#include <iostream>
#define endl '\n'
using namespace std;
using ul = uint64_t;
ul sol(int n) {
if (n == 1) return 0L;
ul res = n;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
res /= i;
res *= (i - 1);
}
while (n % i == 0) n /= i;
}
if (n != 1) {
res /= n;
res *= (n - 1);
}
return res;
}
int main() {
cin.tie(0)->sync_with_stdio(false);
int n;
while (true) {
cin >> n;
if (!n) break;
cout << sol(n) << endl;
}
}
'coding_test > BAEKJOON' 카테고리의 다른 글
| 백준 11689번 C++ 풀이 (0) | 2025.02.07 |
|---|---|
| 백준 19577번 C++ 풀이 (0) | 2025.02.07 |
| 백준 15681번 C++ 풀이 (0) | 2025.02.07 |
| 백준 2258번 C++ 풀이 (0) | 2025.02.06 |
| 백준 11779번 C++ 풀이 (0) | 2025.02.05 |
