https://www.acmicpc.net/problem/15829
15829번: Hashing
APC에 온 것을 환영한다. 만약 여러분이 학교에서 자료구조를 수강했다면 해시 함수에 대해 배웠을 것이다. 해시 함수란 임의의 길이의 입력을 받아서 고정된 길이의 출력을 내보내는 함수로 정
www.acmicpc.net
자료형에 바이트가 정해진건 정말 귀찮다.
그냥 다 더하고 마지막에 나누면 오버플로우가 나게 된다.
이걸 어떻게 해결하지 하다가 포기했던 문제인데, 나머지 연산(모듈러 연산)법칙에 관해 알게되어 어찌저찌 풀게 되었다.
나머지 연산의 법칙중 분배법칙을 이용해서 풀면 된다.

이중 1번째와 3번째를 이용하게 된다. 덧셈에 관한 증명은 여기서(https://sexycoder.tistory.com/66)
여기까지는 다른사람들의 일반적인 설명이지만, 나같은 돌대가리는 이해를 제대로 못해 설명이 더 필요했다. 근데 아무도 안해주더라.....
주어진 해시함수는 다음과 같다.

다음의 해시 함수를 풀어보면
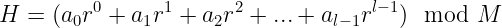
이 된다. 덧셈에 관한 증명법을 살펴보면, a+b+c....로 확장이 가능하다는 것이 보인다. 즉 덧셈에 관해서 항의 개수가 확장이 가능하다. 그래서 덧셈의 분배법칙을 적용하면

이 된다.
이제 안쪽의 모듈러 연산에 곱셈의 분배법칙을 적용하면 다음과 같다.

그런데 이 문제에서 a_i는 M인 1234567891보다 월등히 작기 때문에 다음과 같이 적히게 된다.
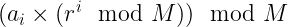
이를 정리해보면 다음과 같아진다.
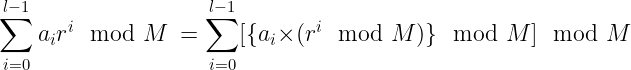
(이게 맞는건가?)
적용해보면 다음과 같다.
#include <stdio.h>
#define r 31
#define M 1234567891
int main () {
int l, i;
char arr[51];
long long hash = 0, R = 1;
scanf("%d %s", &l, arr);
for (i = 0; i < l; i++) {
hash += ((arr[i] - 'a' + 1) * R) % M; hash %= M;
R *= r; R %= M;
}
printf("%lld", hash % M);
return 0;
}또 c++로도 해봤다. 확실히 C언어보다 편의적인 기능이 더 있으니 좋은것 같다.
#include <iostream>
#include <string>
#define r 31
#define M 1234567891
using namespace std;
int main () {
int l, i;
long long hash = 0, R = 1;
string str;
cin >> l >> str;
for (i = 0; i < str.length(); i++) {
hash += ((str[i] - 'a' + 1) * R) % M; hash %= M;
R = (R * r) % M;
}
cout << hash;
}25.03.14 추가
어느순간 보니까 이 글이 내 블로그에서 많이 찾는 글중 하나가 되었다. 나도 다시 읽어보았는데, 링크로 걸어둔 모듈러 연산의 증명에 관한 링크가 사라졌다. 그래서 이 당시의 돌대가리였던 나같은 사람들을 위해 설명을 해보고자 한다.
정수론에서는 나눗셈 정리라는 개념이 있는데, 쉽게 말해 임의의 정수 a는 임의의 정수 b에 대해

로 나타낼 수 있다는 것이다. 이제 A, B를 같은 q에 대해 다음과 같이 나타내보자.

이제 A + B, A - B, A × B는 다음과 같이 표현된다.

q에 대한 나머지를 따져보면, 결국 다음과 같다.

그래서, 각 숫자에 대해 모듈러를 먼저 처리한 후, 원하는 연산을 한 다음에, 또 모듈러를 취해줘도 되는 것이다. 물론 나눗셈에는 적용되지 않는다. 여기서부터는 모듈러 역원이라는 개념이 적용된다.
'coding_test > BAEKJOON' 카테고리의 다른 글
| 백준 2914번 C언어 풀이 (0) | 2021.09.15 |
|---|---|
| 백준 11653번 C언어 풀이 (0) | 2021.09.14 |
| 백준 1002번 C언어 풀이 (0) | 2021.09.12 |
| 백준 3053번 C언어 풀이 (0) | 2021.09.10 |
| 백준 2581번 C언어 풀이 (0) | 2021.09.10 |
