백준 13565번 C++ 풀이

https://www.acmicpc.net/problem/13565

13565번: 침투

시간 제한	메모리 제한	solved.ac 티어
1초	512MB	실버 2

문제

인제대학교 생화학연구실에 재직중인 석교수는 전류가 침투(percolate) 할 수 있는 섬유 물질을 개발하고 있다. 이 섬유 물질은 2차원 M × N 격자로 표현될 수 있다. 편의상 2차원 격자의 위쪽을 바깥쪽(outer side), 아래쪽을 안쪽(inner side)라고 생각하기로 한다. 또한 각 격자는 검은색 아니면 흰색인데, 검은색은 전류를 차단하는 물질임을 뜻하고 흰색은 전류가 통할 수 있는 물질임을 뜻한다. 전류는 섬유 물질의 가장 바깥쪽 흰색 격자들에 공급되고, 이후에는 상하좌우로 인접한 흰색 격자들로 전달될 수 있다.

김 교수가 개발한 섬유 물질을 나타내는 정보가 2차원 격자 형태로 주어질 때, 바깥쪽에서 흘려 준 전류가 안쪽까지 침투될 수 있는지 아닌지를 판단하는 프로그램을 작성하시오.

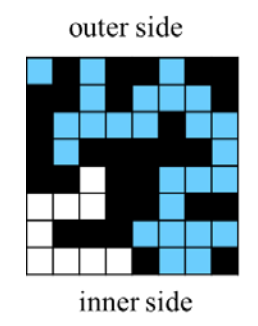(a) The current percolates.	(b) The current does not percolate.

예를 들어, Figure 1(a) 에서는 바깥쪽에서 공급된 전류가 안쪽까지 침투하지만, Figure 1(b)에서는 그렇지 못한다.

입력

첫째 줄에는 격자의 크기를 나타내는  M (2 ≤ M ≤ 1,000) 과 N (2 ≤ N ≤ 1,000) 이 주어진다. M줄에 걸쳐서, N개의 0 또는 1 이 공백 없이 주어진다. 0은 전류가 잘 통하는 흰색, 1은 전류가 통하지 않는 검은색 격자임을 뜻한다.

출력

바깥에서 흘려준 전류가 안쪽까지 잘 전달되면 YES를 출력한다.

그렇지 않으면 NO를 출력한다.

---

 

전형적인 그래프 탐색 문제이다. 맨 아래(inner side)에서 출발하여 맨 위(outer side)로 가는 경로가 있는지 조사하면 된다.

 

#include <bits/stdc++.h>
using namespace std;

int n, m;
vector<vector<int>> graph;

void input() {
    cin >> m >> n;
    graph.resize(m);
    string input;

    for(auto& row : graph) {
        cin >> input;
        for(char x : input) row.push_back(x - '0');
    }
}

// 41192KB / 36ms
bool dfs(int st_x, int st_y) {
    if (st_y == 0) return true;
    graph[st_y][st_x] = -1;

    bool result = false;
    int dx[4] = {1, 0, -1, 0};
    int dy[4] = {0, 1, 0, -1};
    for (int i = 0; i < 4; i++) {
        int next_x = st_x + dx[i];
        int next_y = st_y + dy[i];
        if(next_x < 0 || next_x >= n || next_y < 0 || next_y >= m) continue;
        if (graph[next_y][next_x] == 0) result = result || dfs(next_x, next_y);

        if (result) return true;
    }
    return false;
}

// 6000KB / 20ms
bool bfs(int st_x) {
    queue<pair<int, int>> q;
    int dx[4] = {1, 0, -1, 0};
    int dy[4] = {0, 1, 0, -1};

    q.push({st_x, m - 1});
    graph[m - 1][st_x] = -1;

    while(!q.empty()) {
        auto [cur_x, cur_y] = q.front();
        q.pop();

        if (cur_y == 0) return true;

        for (int i = 0; i < 4; i++) {
            int next_x = cur_x + dx[i];
            int next_y = cur_y + dy[i];
            if(next_x < 0 || next_x >= n || next_y < 0 || next_y >= m) continue;
            
            if (graph[next_y][next_x] == 0) {
                graph[next_y][next_x] = -1;
                q.push({next_x, next_y});
            }
        }
    }
    return false;
}

void sol() {
    for(int x = 0; x < n; x++) {
        if (graph[m - 1][x] == 0) {
            // if (bfs(x)) {
            if (dfs(x, m-1)){
                cout << "YES";
                return;
            }
        }
    }
    cout << "NO";
}

int main () {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    input();
    sol();
}