백준 11660번 C++ 풀이

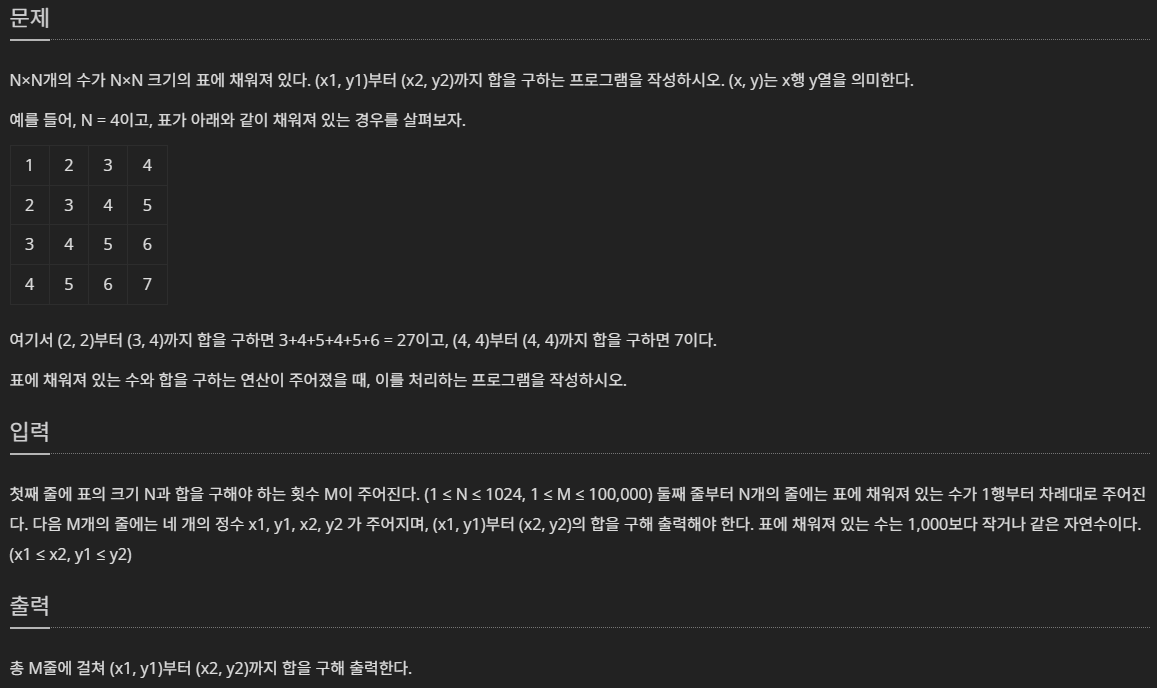
문제

https://www.acmicpc.net/problem/11660

(25.01.14 현재 백준사이트의 미리보기 블록이 만들어지지 않는다.)

 

시간 제한	메모리 제한	solved.ac 티어
1초	256MB	실버 1

---

풀이

본래 구간 합 구하기 문제들은 세그먼트 트리를 사용하는 문제들이 꽤 있는데, 이번 문제는 누적 합 알고리즘을 사용하는 것 만으로도 충분한 문제이다. 각 행에 대해 누적합 배열로 변경한 후, 입력받는 쿼리에 대해 누적합 배열을 이용하면 시간복잡도 안에 끝낼 수 있을 것이다.

문제의 표를 누적합 배열로 바꾸면 다음과 같을 것이다.

1	3	6	10
2	5	9	14
3	7	12	18
4	9	15	22

 

예제입력1의 첫번째 쿼리는 다음과 같다.

2 2 3 4

 

원래라면 해당 쿼리를 처리하기 위해서 다음의 영역의 각 숫자들을 더해야 할 것이다.

1	2	3	4
2	3	4	5
3	4	5	6
4	5	6	7

 

하지만 지금은 표도 작고, 구간의 영역도 작으니 단순 반복문으로 풀어도 되겠지만, 우리는 이미 누적합 배열로 바꿨기 때문에 다음과 같이 바꿀 수 있다. 빨간색은 더하는 값, 초록색은 빼는 값이다.

1	3	6	10
2	5	9	14
3	7	12	18
4	9	15	22

 

이를 문제의 표기법대로 바꾸면 (2,4) + (3,4) - (2,1) - (3,1)로 바꿀 수 있다. 이를 일반화하면 (x1,y2) + (x2,y2) - (x1,y1-1) - (x2,y1-1)이 된다. x1 <= x2임은 입력조건에 따라 자명하기 때문에 누적합 배열에서 [x1, x2] 구간을 반복하면서, (xn, y2)의 값을 더하고, (xn, y1-1)의 값을 빼주면 반복횟수를 줄이면서 원하는 답을 얻을 수 있다.

코드

#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int n, m;
vector<vector<int>> table;
vector<tuple<int,int,int,int>> query;

void input() {
	cin >> n >> m;
	table.resize(n+1, vector<int>(n+1));
	query.resize(m);

	for(int x = 1; x <= n; x++) {
		for(int y = 1; y <= n; y++) {
			cin >> table[x][y];
			table[x][y] += table[x][y-1];
		}
	}

	for(auto& [x1, y1, x2, y2] : query) {
		cin >> x1 >> y1 >> x2 >> y2;
	}
}

void sol() {
	int ans;
	for(auto [x1, y1, x2, y2] : query) {
		ans = 0;

		for(; x1 <= x2; x1++) {
			ans += table[x1][y2];
			ans -= table[x1][y1 - 1];
		}

		cout << ans << endl;
	}
}

int main() {
	cin.tie(0)->sync_with_stdio(0);
	input();
	sol();
}